Bahas Soal Matematika   »     ›  

Himpunan penyelesaian dari \( \sin^2 2x + 4 \sin 2x -5 = 0 \) untuk \( 0^\circ \leq x \leq 360^\circ \) adalah…

1. \( HP = \{ 45^\circ, 225^\circ \} \)
2. \( HP = \{ 45^\circ, 135^\circ \} \)
3. \( HP = \{ 45^\circ, 345^\circ \} \)
4. \( HP = \{ 125^\circ, 225^\circ \} \)
5. \( HP = \{ 135^\circ, 315^\circ \} \)

Pembahasan:

Untuk menyelesaikan persamaan trigonometri ini, kita misalkan \( p = \sin 2x \). Kita peroleh:

Perhatikan bahwa untuk \( p = -5 \Leftrightarrow \sin 2x = -5 \) tidak memenuhi syarat karena \( -1 \leq \sin x \leq 1 \). Untuk \( p=1 \), diperoleh:

Dari persamaan yang diperoleh di atas, kita pilih \(k\) bilangan bulat untuk memperoleh nilai \(x\) yang memenuhi syarat.

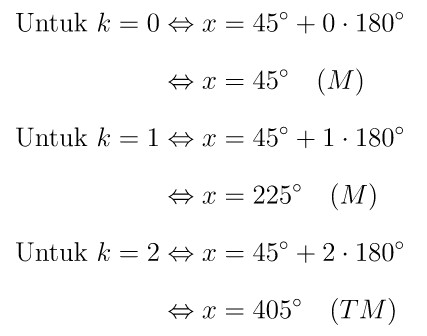
Catatan: Memenuhi (M), Tidak Memenuhi (TM)

Jadi, himpunan penyelesaian dari \( \sin^2 2x + 4 \sin 2x -5 = 0 \) untuk \( 0^\circ \leq x \leq 360^\circ \) adalah \( \{ 45^\circ, 225^\circ \} \).

Jawaban A.